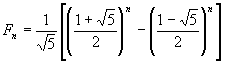|
Una successione è un insieme I di elementi, solitamente della stessa natura, ciascuno dei quali è associato a un numero naturale. Secondo una definizione più rigorosa, una successione è una funzione che associa a ogni numero naturale n un elemento an si un altro insieme (per esempio dei numeri reali). Una successione viene quindi indicata con a0, a1, a2, ..., an, ..., dove 0, 1, 2, ..., n, ... saranno gli indici; una successione è pertanto formata da infiniti elementi elencati in modo ordinato. Uno degli esempi più chiari è la "successione di Fibonacci" in cui ogni elemento (eccetto i primi due) è la somma dei precedenti due (0, 1, 1, 2, 3, 5, 8, ...). Questa successione è nata da un semplice problema posto da Fibonacci: se una coppia di conigli mette al mondo ogni mese una nuova coppia di conigli, che dopo due mesi producono loro volta una nuova coppia di conigli, quante coppie di conigli avremo dopo un anno, se tutti i conigli rimangono in vita? I numeri di Fibonacci sono quindi elementi della successione: F0, F1, F2, F3, ..., Fn, ... Definita ricorsivamente come segue:
La prima riga di questa definizione è detta "delle condizioni iniziali", dove i primi due numeri della successione F0 e F1 sono definiti esplicitamente, mentre la seconda rappresenta la "relazione ricorsiva". I primi termini della successione di Fibonacci si possono quindi calcolare facilmente sommando i primi due:
PARTICOLARITA' Nel 1553 il matematico scozzese P. Simson stabilì che il rapporto tra due termini consecutivi di questa sequenza tende al valore della sezione aurea j = 1,61803 ... I primi rapporti sono:
Dopo 12 termini l'approssimazione della sezione aurea è corretta fino a quattro termini decimali. Inoltre lo scozzese scoprì l'identità: Fn-1Fn+1-Fn2 = (-1)n Nel 1718 il matematico francese A. De Moivre scoprì la formula che definisce direttamente l'n-esimo numero di Fibonacci:
La sequenza di Fibonacci, oltre a rappresentare matematicamente il contenuto armonico della sezione aurea, presenta anche aspetti curiosi e affascinanti. Charles Raine mise in relazione i numeri della sequenza con i triangoli rettangoli pitagorici. Presi infatti quattro numeri consecutivi qualsiasi di Fibonacci, il prodotto dei termini esterni ed il doppio prodotto di quelli interni danno come risultato le misure dei cateti di un triangolo pitagorico. Ad esempio considerando i quattro numeri consecutivi 3, 5, 8 e 13 si ottengono i due cateti 39 e 80 del triangolo pitagorico 39-80-89. L'ipotenusa, 89, è anch'essa un numero della sequenza e l'area di tale triangolo, 1560, è il prodotto dei quattro numeri di partenza (3x5x8x13). K. Subba Rao notò che i numeri della sequenza compresi tra n e 2n sono 1 o 2, e la quantità dei termini di Fibonacci con lo stesso numero di cifre è uguale a 4 oppure a 5. Inoltre due numeri consecutivi di Fibonacci sono sempre primi tra loro e dato F (numero qualsiasi della successione), tra i primi F2 termini della sequenza ve n'è almeno uno divisibile per F. Ponendo ad esempio F=13 nei successivi 169 (F2) termini di Fibonacci ce n'è almeno uno divisibile per 13 (377).
Esiste anche una relazione tra i numeri di Fibonacci e i coefficienti binomiali scoperta da Lucas:
Catalan similmente dimostrò che:
Vi sono inoltre formule che consentono di determinare la somma dei primi n termini della successione di Fibonacci (a), nonché le somme dei termini di pedice dispari (b) e pari (c)
|
||||||||||||||||||||||||||||||||