Curiosità sui numeri:
IL NUMERO D'ORO j =1,61803398874989...
Dietro l'idea di armonia e di
perfezione, nella natura come nell'arte, si nasconde un numero il cui valore
non è esprimibile in cifre decimali se non in forma approssimata: 1,618034... Si tratta infatti di un numero
irrazionale, o meglio di un numero trascendente che è, con pi greco (p), il più
celebre fra i numeri di questa specie. E' il numero
d'oro, che all'inizio del secolo scorso, il matematico americano Mark Barr
propose di indicare con la lettera greca "j",
dall'iniziale di Fidia, il grande scultore greco che lo ebbe sempre presente
nel realizzare le sue sculture e nella costruzione del Partenone di Atene.
Il rapporto 1:1,618.. è stato, sin dai tempi più antichi, preso in
considerazione per costruire opere la cui armonia é dettata dalla "divina
proporzione" tanto da nominarla Sezione
aurea.
Il
suo
valore esatto è:
che corrisponde alla soluzione positiva dell'equazione di secondo grado:
|
j2
-j
- 1 |
Come p, j può essere espresso anche come somma di una serie infinita.
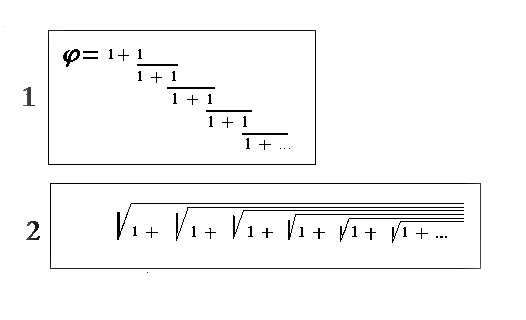
Se con la calcolatrice digitiamo 1+1 e sottoponiamo la somma al suo reciproco (1/x) otterremo 0,5 al quale sommiamo ancora 1 e poi ancora il reciproco, 1/(0,5+1). Ripetendo più volte la stessa procedura, otterremo come risultato un numero che sempre più si si avvicinerà al numero d'oro. ( vedi formula 1).
Un secondo metodo, sempre con la calcolatrice, è partire ancora da 1+1, ed elevare il risultato alla radice quadrata. Ripetendo la stessa operazione n volte, otterremo un numero molto vicino al numero d'oro (dopo l'undicesima radice si ottiene 1,618034). ( vedi formula 2).
Tra le numerose proprietà del numero aureo, il j è l'unico numero positivo che mantiene le stesse cifre decimali anche nel proprio reciproco,
Infatti 1/1,618034 = 0,618034..... (provare per credere!).
Una seconda forma del numero d'oro, dove la parte decimale rimane inalterata, è:
|
j2 = j + 1 |
Infatti 1,6180342 =2 ,618034.
Vedi anche l'argomento SEZIONE AUREA