

Sin dai tempi più antichi, dagli egiziani ai più moderni frattali, esiste una proporzione divina (o sezione aurea) che è stata presa in considerazione
per ottenere una dimensione armonica delle cose. Dalla geometria all'architettura, dalla pittura alla musica, fino alla natura del creato possiamo osservare come tale rappresentazione corrisponda ad un rapporto che è stato definito pari a 1,618...(numero d'oro)
- La piramide egizia di Cheope ha una base di 230 metri ed una altezza di 145: il rapporto base/altezza corrisponde a 1,58 molto vicino a 1,6.
- Nei megaliti di Stonehenge, le superfici teoriche dei due cerchi di pietre azzurre e di Sarsen, stanno tra loro nel rapporto di 1,6.
- La pianta del Partenone di Atene è un rettangolo con lati di dimensioni tali che la lunghezza sia pari alla radice di 5 volte la larghezza, mentre nell'architrave in facciata il rettangolo aureo è ripetuto più volte.
- Anche nella progettazione della Cattedrale di Notre Dame a Parigi e del Palazzo dell'ONU a New York sono state utilizzate le proporzioni del rettangolo aureo.
- Nelle arti del passato, in molte opere di Leonardo da Vinci, Piero della
Francesca, Bernardino Luini, Sandro Botticelli, si ricorreva spesso alla sezione
aurea (la divina proportione), considerata quasi la chiave mistica
dell'armonia nelle arti e nelle scienze.
-Anche nella musica, Beethoven, nelle "33 variazioni sopra un valzer di Dabelli" suddivise la sua composizione in parti corrispondenti corrispondenti ai numeri di Fibonacci, il cui rapporto corrisponde al numero d'oro.
Un largo contributo alla conoscenza ed alla divulgazione di questo metodo di suddivisione armonica è stato dato dal matematico Luca Pacioli con la pubblicazione del libro De divina Proportione, testo illustrato con disegni di Leonardo Da Vinci.
Fu nell'Ottocento che alla "Divina proporzione" venne dato il nome di "Sezione aurea".
Negli oggetti quotidiani, possiamo trovare alcuni esempi di sezione aurea:dalle schede telefoniche alle carte di credito e bancomat, dalle carte SIM dei cellulari alle musicassette: sono tutti rettangoli aurei con un rapporto tra base ed altezza pari a 1,618.
In natura il rapporto aureo è riscontrabile in molte dimensioni del corpo umano. Se moltiplichiamo per 1,618 ladistanza che in una persona adulta e proporzionata, va dai piedi all'ombelico, otteniamo la sua statura. Così la distanza dal gomito alla mano (con le dita tese), moltiplicata per 1,618, dà la lunghezza totale del braccio. La distanza che va dal ginocchio all'anca, moltiplicata per il numero d'oro, dà la lunghezza della gamba, dall'anca al malleolo.Anche nella mano i rapporti tra le falangi delle dita medio e anulare sono aurei, così il volto umano è tutto scomponibile in una griglia i cui rettangoli hanno i lati in rapporto aureo.



Metodo analitico per la determinazione del rapporto aureo
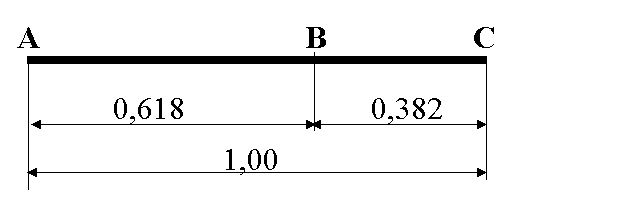
Dato un segmento (AC), si ottiene una sezione aurea quando il tratto più corto (BC) sta al tratto più lungo (AB) come il tratto più lungo (AB) sta al segmento intero (AC).
In sintesi la proporzione è così espressa:
|
BC: AB=AB: AC |
Per avere l'idea della proporzione se consideriamo la misura del segmento pari all'unità, possiamo calcolare la misura dei due tratti AB e BC:
AB + BC= 1 e BC = AB*AB/AC
Quindi: BC = 1-AB e 1 - AB= AB2/1
che si risolve come equazione di secondo grado:
AB2 + AB -1= 0 AB= [-1 ±RADQ (1+4 )]/2
e si ottiene: AB= (-1 + RADQ 5 )/ 2 = (-1 + 2,236068) /2 = 0,618034...
e BC= 1-0,618034= 0,381966...
che corrisponde ad un rapporto uguale a: 0,618034/0,381966= 1,618034...
- Le prime 12 frazioni con numeratore sino a 1000, che più si avvicinano a questo rapporto sono:
| 233/144= 1,618056 | 377/233= 1,618026 | 466/288= 1,618056 |
| 521/322= 1,618012 | 610/377=1,618037 | 665/411= 1,618005 |
| 699/432=1.618056 | 754/466=1.618026 | 843/521=1.618042 |
| 898/555=1.618018 | 932/576=1.618056 | 987/610=1.618033 |
C'è un metodo per ottenere dei numeri che se rapportati tra loro danno come risultato un numero che si avvicina sempre più al numero d'oro man mano che i numeri diventano grandi.
Questi numeri sono quelli appartengono alla serie di Fibonacci una serie in cui ogni termine si ottiene dalla somma dei due precedenti.
I primi elementi sono pertanto:
1,1,2,3,5,8,13,21,34,55,89,144,.......
A partire da tale successione, se formiamo una serie di tipo frazionario, emergono i seguenti rapporti:
1/1; 2/1; 3/2; 5/3; 8/5; 13/8; 21/13; 34/21; 55/34, 89/55; 144/89 ecc.
i cui valori decimali approssimati sono:
1; 2; 1,5; 1, 666; 1,6; 1,625; 1,615; 1, 619; 1, 617; 1, 6181; 1, 6180 ecc.
COSTRUZIONE DEL SEGMENTO AUREO
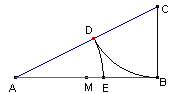
Dato il segmento AB, dividerlo in due parti uguali con il punto M. Dall'estremità B tracciare la perpendicolare al segmento fino al ottenere CB= MB.
Dal punto C, tracciare con il compasso un semicerchio fino ad incontrare in D il segmento AC. Puntando infine il compasso in A con raggio AD, si ottiene il punto E che divide il segmento in due parte con proporzione aurea (AE/EB= 1,618).
TRIANGOLO CON ANGOLI DI MISURA: 72°, 72°, 36°.
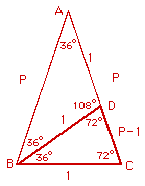 Dato
un triangolo isoscele i cui angoli alla base misurano 72° ciascuno, e
l’angolo al vertice misura 36°, la bisettrice di un angolo alla base divide
il lato obliquo opposto nel punto d’intersezione in due segmenti in modo tale
da creare una sezione aurea. Infatti il triangolo ABC è simile al triangolo
BCD. E da questo risulta che:
Dato
un triangolo isoscele i cui angoli alla base misurano 72° ciascuno, e
l’angolo al vertice misura 36°, la bisettrice di un angolo alla base divide
il lato obliquo opposto nel punto d’intersezione in due segmenti in modo tale
da creare una sezione aurea. Infatti il triangolo ABC è simile al triangolo
BCD. E da questo risulta che:
AC:BC=BD:DC e dunque: AC:AD=AD:DC
TRIANGOLO CON ANGOLI DI MISURA: 36°, 36°, 108°.
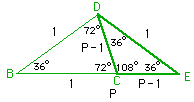
Dato un triangolo isoscele i cui angoli alla base misurano 36° ciascuno, e l’angolo al vertice misura 108°, il lato obliquo e la differenza tra la base e il lato obliquo danno vita a una sezione aurea. Infatti il triangolo CDE è simile al triangolo ABD della figura precedente.
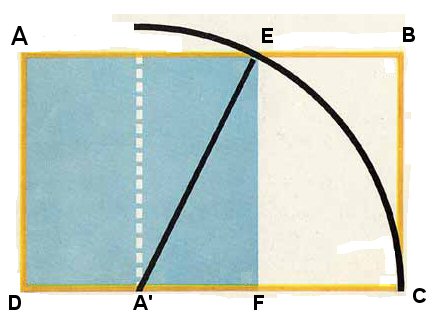 Esiste uno speciale rettangolo le cui proporzioni
corrispondono alla sezione aurea. Il suo nome è rettangolo aureo. Per costruire
il rettangolo aureo si disegni un quadrato di lato a i cui vertici chiameremo, a
partire dal vertice in alto a sinistra e procedendo in senso orario, AEFD.
Quindi dividere il segmento AE in due chiamando il punto medio A'. Utilizzando
il compasso e puntando in A' disegnare un arco che da E intersechi il
prolungamento del segmento DF in C. Con una squadra disegnare il segmento CB
perpendicolare ad DF, ed il segmento EB, perpendicolare a EF. Il rettangolo ABCD è un rettangolo aureo nel quale
il lato AB è
diviso dal punto E esattamente nella sezione aurea:
Esiste uno speciale rettangolo le cui proporzioni
corrispondono alla sezione aurea. Il suo nome è rettangolo aureo. Per costruire
il rettangolo aureo si disegni un quadrato di lato a i cui vertici chiameremo, a
partire dal vertice in alto a sinistra e procedendo in senso orario, AEFD.
Quindi dividere il segmento AE in due chiamando il punto medio A'. Utilizzando
il compasso e puntando in A' disegnare un arco che da E intersechi il
prolungamento del segmento DF in C. Con una squadra disegnare il segmento CB
perpendicolare ad DF, ed il segmento EB, perpendicolare a EF. Il rettangolo ABCD è un rettangolo aureo nel quale
il lato AB è
diviso dal punto E esattamente nella sezione aurea:
AE:EB=AB:AE
PENTAGONO E TRIANGOLI IN ESSO CONTENUTI
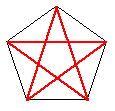 All’interno
di un pentagono, ogni lato forma con due diagonali (il segmento che unisce due
punti non adiacenti) un triangolo dagli angoli con misura 72°, 72°, 36°, con
le proprietà spiegate in precedenza. Ogni lato forma, con il punto d’incontro
di due diagonali consecutive, un triangolo dagli angoli 36°, 36°, 108°, con
le proprietà descritte in precedenza. Cioè il lato del pentagono regolare è
la sezione aurea di una sua diagonale e il punto d' intersezione tra due
diagonali divide ciascuna di esse in due segmenti che stanno nel rapporto aureo.
All’interno
di un pentagono, ogni lato forma con due diagonali (il segmento che unisce due
punti non adiacenti) un triangolo dagli angoli con misura 72°, 72°, 36°, con
le proprietà spiegate in precedenza. Ogni lato forma, con il punto d’incontro
di due diagonali consecutive, un triangolo dagli angoli 36°, 36°, 108°, con
le proprietà descritte in precedenza. Cioè il lato del pentagono regolare è
la sezione aurea di una sua diagonale e il punto d' intersezione tra due
diagonali divide ciascuna di esse in due segmenti che stanno nel rapporto aureo.
Il pentagono stellato è sicuramente la figura geometrica che più di ogni altra rappresenta, all'infinito, la sezione aurea. E' forse per questo motivo che questo fu scelto come simbolo della scuola pitagorica.
SPIRALE AUREA
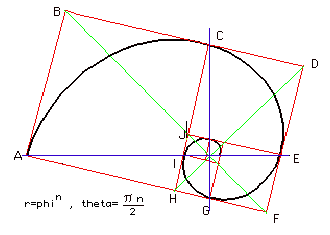
Se all’interno di un rettangolo aureo si disegna un quadrato con lato uguale al lato minore del rettangolo, il rettangolo differenza sarà anch’esso un rettangolo aureo. Si ripeta l’operazione per almeno cinque volte al fine di avere un effetto visivo adeguato. Si punti la punta del compasso sul vertice del quadrato che giace sul lato lungo del rettangolo e si tracci l’arco che unisce i gli estremi dei due lati che formano l'angolo scelto. Si ripete l'operazione per ogni quadrato disegnato in modo da creare una linea continua.